문제

나리는 당첨 상품이 {자동차, 유럽 여행, 백화점 상품권, 꽝}인 경품 행사에 참가하려고 한다. 각각의 결과에 대한 나리의 기대효용은 U(자동차)=100, U(유럽 여행)=80, U(백화점 상품권)=30, U(꽝)=0이다. 이때 A안은 각각 당첨 상품이 나올 확률이 {1/2, 0, 0, 1/2}이고 B안은 {1/4, 1/4, 1/4, 1/4}이다. 나리는 어느 안을 선호하겠는가? 또한 A안과 B안의 기대효용은 얼마인가?
[국가공인 1호 한경 TESAT] 기대효용
해설

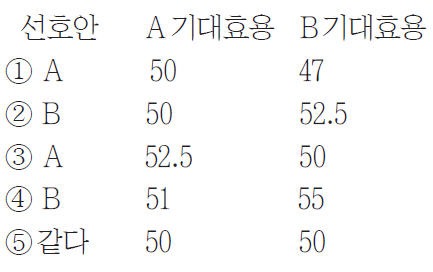
복권·경품 행사 당첨과 같이 소비행동의 결과가 불확실한 경우가 있다. 이때 불확실한 결과 간의 선호를 효용으로 나타낸 ‘효용의 기댓값’을 기대효용 또는 폰 노이만-모르겐스턴 효용지표(von Neumann Morgenstern utility index)라 한다. 지문의 경품 상품이 나올 확률과 각각 경품 상품에 대한 효용값을 곱한 후 모두 더하면 A안과 B안의 기대효용을 구할 수 있다. A 기대효용은 100×1/2=50, B 기대효용은 (100+80+30)×1/4=52.5다.

따라서 B안의 기대효용값이 더 크므로 나리는 B안을 선호한다.

정답 (2)