유전학 전문가 "생명과학Ⅱ 20번, 과학적 오류가 명백한 문제" [전문]

출제오류 논란이 불거진 수능 생명과학Ⅱ 문항을 둘러싼 첫 법정공방이 열린 지난 8일 오후 한국교육과정평가원을 상대로 집행정지를 신청한 수험생들이 서울 서초구 서울행정법원에서 열린 심문이 끝난 뒤 법정에서 나와 기자회견을 하고 있다. 연합뉴스.

‘수능 성적 통지 연기’라는 사상 초유의 사태가 벌어진 가운데 생명과학 전문가들도 한국교육과정평가원의 주장이 납득이 가지 않는다는 입장이다.

10일 법조계에 따르면 지난 9일 서울행정법원 행정6부(부장판사 이주영)는 수능 과학탐구 영역 생명과학Ⅱ 과목의 응시자 등 92명이 한국교육과정평가원을 상대로 낸 수능 정답결정처분 취소 집행정지 사건에서 인용 결정을 내렸다. 이에 따라 본안 소송 판결이 나오기 전까지 생명과학Ⅱ 과목을 택한 응시자 6515명의 성적표는 해당 부분만 공란으로 처리해 배부한다. 수능 문제 오류에 대해 법원이 가처분 신청을 인용한 것은 물론 성적표 일부분이 공란으로 배부되는 것은 사상 처음이다.

2022학년도 대학수학능력시험 과학탐구영역 생명과학2 20번 문항. 한국교육과정평가원 제공.

생명과학Ⅱ 20번 문항은 동물 종 P의 두 집단이 지닌 유전적 특성을 분석해 ‘멘델 집단’을 가려내는 문제다. 이의를 제기한 수험생들은 “지문대로 계산하면 동일집단의 개체 수가 음수가 되는 오류로 인해 문제를 풀 수 없다”고 주장했다. 평가원은 수능 채점 결과를 발표하면서 생명과학Ⅱ 출제 오류 논란에 대해 ‘이상 없다’는 입장을 재차 확인했다.

김종일 서울대 유전체의학연구소장 겸 의과대학 의과학과장은 지난 9일 한국경제신문과의 인터뷰에서 “평가원이 문제 오류를 미리 발견하지 못한 ‘직무유기’를 했다고 생각한다”고 밝혔다.

이하 김종일 서울대 유전체의학연구소장의 입장 전문.

"평가원이 틀린 문제를 낼 수도 있고 그 결정은 웬만해서는 뒤집어지지 않는다는 교훈을 남기게 될 것"

안녕하십니까? 저는 서울대학교 의과대학에서 의과학과장과 유전체의학연구소장을 맡고 있는 김종일입니다. 이번에 논란이 되고 있는 2022년 수학능력시험 생명과학II 20번 문제에 대하여 제 의견을 밝히고자 메일을 드립니다. 먼저 아래의 의견은, 제 개인적인 견해일 뿐, 서울대학교의 공식 입장과는 무관함을 먼저 밝힙니다.

저는 학부생과 대학원생을 대상으로 유전학, 유전체학 강의를 하고 있고, 하디-바인베르크 평형에 대해서도 강의를 하고 있습니다. 올해에도 2학기에 의학과 대학원생을 대상으로 하는 ‘유전체의학 개론’ 강의에서 1시간 동안 하디-바인베르크 평형에 대한 수업을 진행한 바 있습니다. 이 문제의 오류를 판단할 수 있는 전문성은 충분하다고 자부합니다.

제가 왜 개인적인 의견을 밝히고자 하는지 먼저 설명드리겠습니다. 제가 아는 한 주위 친인척 중에서 올해 수능을 보는 사람은 없습니다. 저는 이 문제와 관련해서 직접적인 이해관계를 가지고 있지 않습니다. 범위를 넓혀서 제 지인들 중에서는 이 문제로 손해를 본 사람, 또 그렇지 않은 사람들이 있겠지만 저는 그 분들 의사를 반영해서 이렇게 편지를 쓰고 있지는 않습니다. 제가 강의하는 분야와 관련이 되어서 호기심을 가지고 문제를 풀어보았고, 제가 속한 학회로 이 문제에 대한 질의가 와서 학회 임원들과 의견을 나누는 과정에서 이 문제에 관심을 가지게 되었습니다. 저는 이 문제가 오류를 가지고 있다고 강력하게 주장하였지만, 학회(제가 속한 여러 학회 중 어느 학회인지는 밝히지 않겠습니다)에서는 괜한 논란에 휩쓸리지 않는 편이 좋겠다는 의견이 더 많아서 공식적인 의견을 밝히지 않기로 결정하였습니다. 제가 속한 학회를 포함하여 몇몇 학회의 의견이 비슷하게 모아진다는 이야기를 전해듣고 나서, 학회가 의견을 표시하지 않는 것이 ‘이 문제와 관련된 귀찮은 일에 휘말리기 싫으므로 의견을 표명하지 않겠다’임에도 불구하고, ‘문제의 오류가 없다’는 의견 표명으로 받아들여질까봐, 대한민국의 ‘전문가’ 중에서 저와 같은 의견을 가진 사람이 최소한 한 명은 있다는 ‘기록’을 남기기 위하여 이러한 메일을 쓰게 되었습니다.

이 문제의 풀이에 대한 자세한 내용은 적지 않겠습니다. (필요하시다면 보내드리겠습니다) 이 문제에서 논란은 2가지 측면에서 보아야 한다고 생각합니다.

첫 번째는 이 문제에서 기술된 제시문에 오류가 있는가 하는 점입니다. 이는 명확합니다. 큰 오류가 있습니다. 만약 제시문의 조건을 그대로 주고 ‘이러한 제시문의 조건을 충족하는 집단이 존재할 수 있는가’라는 문항이 수학능력시험에 출제된다면 ‘존재할 수 없다’가 정답입니다. 이러한 내용에 대하여 각 전문가나 학회에 질의를 한다면 ‘답을 하기 싫다’와 ‘존재할 수 없다’의 답변만 나오지, ‘존재할 수 있다’라고 대답할 전문가는 한 명도 없다는 것을 확신합니다. 단순한 오탈자 하나도 나오지 않도록 합숙하면서 검토를 반복하는 수학능력시험 문제에 이렇게 명백한 과학적 오류가 있다는 것 자체가 심각한 문제임에도 불구하고, 많은 전문가들이 두 번째 측면의 문제 때문에 답을 꺼리다보니 제시문에 명백한 오류가 있다는 사실이 묻히는 것 같아 안타깝습니다.

두 번째 측면은, 이 오류가 정답을 푸는 과정과 관련이 있는가 하는 점입니다. 아무래도 이 측면 때문에 논란이 심해지고 있고, 전문가들이 답을 꺼리고 있다고 생각합니다. 제 개인적인 견해는, 이 문제에 대한 해답도 명확하다(문제 푸는 과정과 관련이 있다)는 것입니다. 예를 들어 단순한 오탈자처럼, 정답을 푸는 과정과 완전히 무관한 오류라면, 이런 일이 발생한 것에 대해서 유감이 있기는 하겠지만 논란은 안 생길 것입니다. 정답을 푸는 과정과 관련이 있을 수 있기 때문에 논란이 되는 것입니다.

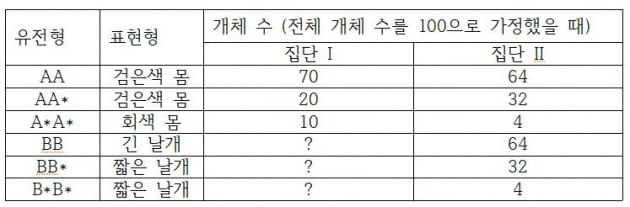
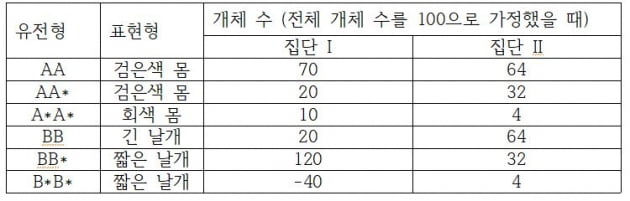
문제에 대해서 조금만 설명을 드리면, 집단 I과 집단 II에서 각각 ‘검은 색 몸’, ‘회색 몸’을 결정하는 대립유전자 빈도와 개체 수, 그리고 ‘긴 날개’, ‘짧은 날개’를 결정하는 대립유전자 빈도와 개체 수를 가지고 제시문의 조건에 따라 적절한 답을 찾는 문제입니다. 여기에서의 오류는, 제시문의 조건대로라면 집단 I에서 ‘긴 날개’, ‘짧은 날개’ 개체 수 중 음수가 나온다는 것입니다. 그런데 문제를 풀다보면 집단 I에서 ‘긴 날개’, ‘짧은 날개’ 개체 수를 구하지 않고도 문제가 풀릴 수 있습니다. 그래서 평가원에서는 ‘학업 성취 수준을 변별하기 위한 평가 문항으로서의 타당성은 유지된다’라고 결정한 것 같습니다.

하지만 저는 이러한 판단에 심각한 문제가 있다고 생각합니다. 이번에 논란이 된 문항은 ‘답을 찾아내기는 어렵지만 주어진 답이 맞는지 검산하는 것은 상대적으로 쉬운 문제’에 속합니다. 주어진 조건을 가지고 각 집단의 대립유전자 빈도 수, 개체 수를 계산하는 과정에는 2차방정식을 몇 개나 풀어야 하는 복잡한 과정이 필요하지만. 한번 개체 수만 구하고 나면 그 다음에는 그 답이 맞는지 주어진 조건과 하나씩 맞추어보기만 하면 됩니다. 즉 아래 테이블을 채우는 것이 어렵지 채우기만 하면 그 다음에는 검산하는 과정이 매우 쉽습니다.

김종일 유전체의학연구소장 제공.

그런데 제시문 내용 중에 ‘짧은 날개 개체 수/검은색 몸 개체 수는 I에서 8/9’라는 조건이 분명하게 있으므로 이를 계산해보기 위해서는 필연적으로 집단 I에서 긴 날개와 짧은 날개 개체수를 계산해야 하고, 그러다보면 다음과 같이 음수 값이 나온다는 것을 알게 됩니다.

김종일 유전체의학연구소장 제공.

전체 개체 수가 100인데 특정 유전형을 가진 개체수가 120 또는 –40이라는 결과를 받아본 학생들은 어떻게 생각할까요?
(가) 제시문의 모순이 있지만 그 모순을 반영하지 않아도 문제가 풀리도록 출제하였을 것이다.
(나) 제시문의 모순이 있을 리 없으므로 내가 푼 계산 과정 어딘가에 오류가 있을 것이다 다시 풀어보아야 되겠다

여기까지 생각한 학생들의 대부분은 (나)를 선택했을 것이라고 확신합니다. 문제를 여러번 다시 풀어도 오류가 확실하다면 그 때 (가)를 고민하겠지요. 그런데 수학능력시험은 이렇게 여러번 다시 풀어볼만큼 시간을 충분히 주지 않습니다.

결국 평가원의 결정은, 우연히 집단 I의 긴 날개/짧은 날개 개체 수를 계산하지 않고 답을 푼 학생, 그리고 다시 검산할 만큼의 시간 여유가 없었던 학생들만 ‘적절한 학업 성취 수준’을 가졌다고 판단한다는 것입니다. 그리고 위와 같이 간편한 검산 방법 대신에 복잡한 2차 방정식을 다시 풀어보는 방식으로 검산한 학생의 손을 들어준 결정입니다. (저는 이렇게 동일한 방법을 반복하면서 자신의 결과를 검토하는 학생보다 다른 방식으로 자신의 결과를 검토하는 학생이 훨씬 우수한 학생이라고 생각합니다) 평가원이 과학적으로 명백한 오류를 가진 문제를 출제했을 리가 없다고 믿고 문제 풀이를 반복하다가 시간을 다 쓴 학생들만 손해를 본 결정입니다.

무엇보다도, 이 기출문제를 풀어본 학생들은 내년부터 어떻게 수학능력시험을 준비해야할까요? 만약 문제를 풀다가 모순을 발견하여도, 그 모순이 답에 영향을 주는 모순인지, 아니면 그걸 무시해도 문제가 풀리는 모순인지를 한 번 더 고민해야 할 것입니다. 평가원이 틀린 문제를 낼 수도 있고 그 결정은 웬만해서는 뒤집어지지 않는다는 교훈을 남기게 될 것입니다. 이 과정에서 우리 어른들이 어린 학생들에게 심어주는 불신감은, 수학능력시험 성적을 다시 매기는 것보다 훨씬 더 큰 손해를 우리 사회에 끼칠 것이라고 생각합니다.

2021년 12월 9일
서울대학교 의과대학 김종일 드림.

김남영 기자 nykim@hankyung.com