허준이 교수가 푼 11개 난제, 어떻게 산업을 발전시키나 [김진원의 머니볼]

"AI학습 비약적으로 개선하는 길 열었다"

허준이 한국 고등과학원 석학교수(미국 프린스턴대 교수·39)가 한국 수학자로는 사상 최초로 ‘수학계 노벨상’으로 알려진 필즈상을 수상했습니다.

허 교수가 수십년간 풀리지 않고 있었던 ‘리드 추측’부터 ‘엘리아스-프라우드풋-웨이크필드’ 추측까지 11개의 난제를 조합론과 대수기하학을 융합한 완전히 새로운 방식으로 풀어냈다는 것이 수상의 주 이유 입니다.

허 교수가 풀어낸 난제들이 무엇인지, 현대 산업계에 미치는 영향은 무엇일지 허 교수의 석사지도교수 김영훈 서울대 수리과학부 교수의 설명과 함께 살펴봤습니다.

세계 수학계가 인정할만큼 최첨단의 연구 성과를 글로 풀어 전달하는데 한계가 있습니다. 비유와 생략이 일부 이뤄진 점은 감안하고 읽어주시면 감사할 것 같습니다.

또 기사 작성 과정에 한국과학기술한림원과 김영훈 교수의 도움을 많이 받았습니다. 한림원과 김 교수에게도 깊은 감사의 뜻을 전합니다.

○1852년 ‘4색 문제’에서 출발
리드 추측에 대해서 이해하기 위해선 먼저 ‘4색 문제’를 통한 설명이 필요합니다. 4색 문제는 1852년 영국 수학자 드모르간이 받은 질문에서 발전한 문제입니다. ‘평면 지도를 4가지 색만 써서 모든 국가를 구별해 색을 칠할 수 있는지’가 주 내용입니다. 이웃한 두 국가는 같은 색을 써서는 안 됩니다.

이 문제는 ‘채색다항식’으로 발전했습니다. 채색다항식은 각 국가를 점으로 표현하고, 인접한 국가들은 선으로 연결하는 방식입니다. 점의 개수와 점에 넣을 수 있는 색의 개수를 수식으로 계산했습니다.

그리고 점의 개수를 늘려가며 수식을 풀어본 결과 수식에 들어가는 숫자들이 서서히 증가하다가 감소하는 패턴을 보였습니다. 예를 들어 1→4→6→3 과 같은 순서입니다.

여기에서부터 ‘리드의 추측’이 나옵니다. 1968년 영국 수학자 도널드 리드는 채색다항식의 숫자들을 앞에서부터 따졌을때 증가하다가 감소한다는 내용의 추측을 제시했습니다.

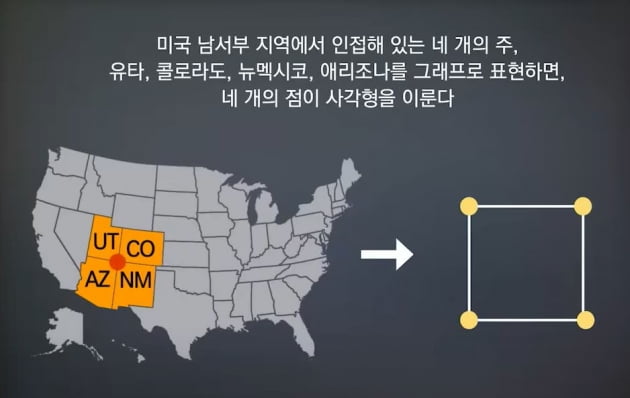
그리고 이 추측은 1974년 ‘호가의 추측’으로 강화됐습니다. 채색다항식의 숫자들을 그림으로 나타내면 밥그릇을 뒤집어 놓은 모양의 아래로 오목한 ‘로그(log)-오목’한 모습을 그린다는 추측을 제시했습니다.

○점과 점을 선으로 연결…‘로그-오목’ 증명
‘로그-오목’의 개념은 수학자들이 오랜 시간 고민해 오던 주제였습니다. 왜냐하면 자연에서 발생한 많은 일들을 수식으로 옮겼을 때, 그 수식에서는 ‘로그-오목’한 모습이 나왔기 때문입니다.

허 교수가 풀어낸 메이슨-웰시 추측, 강한 메이슨 추측, 로타 추측, 브리로스키 추측, 도슨-콜번 추측 모두 특정 수식에서 나오는 ‘로그-오목’과 관련이 있습니다.

김 교수는 “허 교수 연구 성과를 한 줄로 보여줄 수 있는 표현”이라며 “자연에서 얻는 모든 ‘로그-오목’ 수열의 뒤에는 이를 설명하는 구조가 존재한다”고 설명했습니다.

허 교수는 11개 난제들에 조합론과 대수기하학에서 나오는 ‘그래프’와 ‘매트로이드’ 개념을 적용했습니다.

쉽게 말해, 그래프는 점과 점을 선으로 연결하는 방식과 관련된 것이다. 한 붓 그리기가 기초적인 그래프 중 하나입니다. 서울 지하철 노선도도 그래프로 볼 수 있습니다.

매트로이드는 점과 점이 모두 연결 돼 있을 경우엔 의존적으로 보고, 연결돼 있지 않을 경우엔 독립적이라고 표현하는 것과 관련 돼 있습니다.

허 교수는 두 개념을 이용해 ‘로그-오목’ 성질이 다양한 수식에 있다는 것을 증명했습니다.

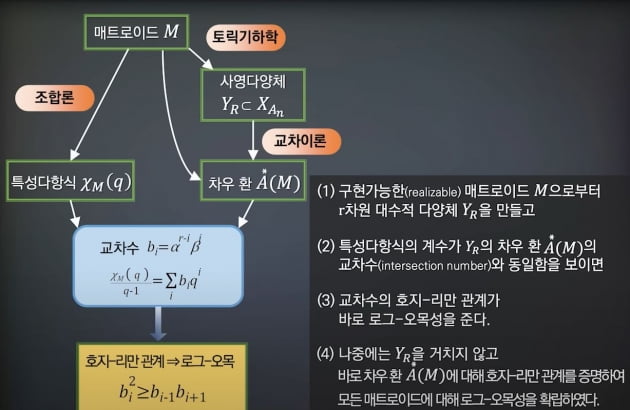
김 교수는 “허 교수가 증명한 각 추측들이 바로 어디에 활용된다고 하는 것은 성급하지만 앞으로 100년 동안 정보통신(IT)과 인공지능(AI) 기계학습, 반도체 설계, 교통-물류 연구에 응용될 것”이라고 했습니다.

○수식 증명으로 IT·AI·반도체 효율성 높일 전망

그래프 이론은 네트워크를 그림으로 그린 수학적 개념입니다. 점과 점이 선으로 연결되는지(의존적), 안 되는지(독립적)를 나타냅니다. 실생활에 가장 가까운 형태로 응용되는 것은 구글 페이지 랭킹입니다.

김 교수는 “예를 들어 ‘한국경제신문’을 키워드를 구글에서 검색하면 ‘한국경제신문’ 단어가 들어간 웹페이지들이 모두 각각의 점이 되고, 각 점을 연결한 게 선이 된다”고 했습니다.

이어 “그래프 이론을 적용해서 모든 선들에 점수를 매겨 우선 순위를 얻은 뒤 가장 점수가 높은 원하는 검색결과를 1페이지 보여주는 방식”이라고 했습니다. 허 교수의 연구를 응용하면 검색 페이지 결과의 정확도를 더욱 높일 수도 있습니다.

AI를 학습시키는 것의 효율성도 크게 높일 수 있을 전망입니다. 이를테면, ‘고양이 사진’을 AI에게 카메라를 통해 보여주고, 모니터에 ‘고양이 단어’를 출력하게 하는 경우를 가정해 봅니다.

고양이 사진과 단어는 각각 하나의 점으로 표현할 수 있습니다. 이 둘은 선으로 연결됩니다. ‘강아지 사진’과 ‘고양이 단어’는 연결시키지 않습니다.

그리고 이 과정을 수없이 많이 반복하면서 학습하고 효율화하는 것이 AI 학습이라고 할 때, 이를 최대한 간단한 수식 하나로 표현 할 수 있다면 인공지능의 효율성이 크게 높아지는 식입니다. 허 교수의 연구가 응용 가능한 분야입니다.

이외에도 수많은 트랜지스터의 집합체인 반도체를 어떻게 효율적으로 연결시킬지, 교통물류 관점에서 점 하나인 트럭 한 개를 수많은 선들로 볼 수 있는 길들 중 어떤 길을 통과 시킬 때 가장 효율적으로 배달 할 수 있는지 등도 관련됩니다.

김 교수는 “필즈상 수상과 같은 수학 분야 최정상급 연구는 수십년에 걸쳐 활용된다”고 했습니다.

그는 “19세기 나온 리만기하학 50년 뒤에 아인슈타인의 상대성이론이 이어졌고, 그 뒤 50년이 지나고 위성항법장치(GPS)가 나오고 인공위성이 날아다니는 세상에 우리는 살고 있다”고 덧붙였습니다.

김진원 기자