이상 '건축무한육면각체' 물리학으로 풀어…"이과가 이과했다"

'삼차각' '육면각' 등 4차원 기하학 기반으로 해설
이수정 GIST 교수·오상현 UC머세드 박사과정생 연구

시인 이상과 그가 프랑스어와 일본어 등을 섞어 발표한 시 '건축무한육면각체'를 한국어로 옮긴 글.

근대 난해시의 대표 격인 이상(1910~1937)의 시 제목과 시구 일부를 4차원 기하학으로 해석하는 시도가 나왔다. 이상의 1931년작 '삼차각설계도' 중 '삼차각'의 의미를 수학적으로 해석하는 식이다. 건축학을 공부한 이상은 '삼차각', '무한육면각체' 등 난해시에 자신이 만든 신조어를 쓴 것으로 유명하다.

광주과학기술원(GIST)에 따르면 이수정 GIST 기초교육학부교수는 오상현 미국 캘리포니아대 머세드 물리학 박사과정생과 최근 발표한 논문에서 이상의 난해시에 등장하는 조어 '삼차각', '육면각' '무한육면각체' 등을 기하학을 기반으로 해설했다.

"이상의 시, 글로 4차원 시공간 구현하려는 시도였다"

두 연구자는 '삼차각'을 4차원 공간상의 방향을 초구면좌표계로 나타낼 때에 쓰이는 세 개의 각도값을 의미한다고 해석했다. 이상이 세 개의 각도값이 하나의 '3차원 각도'를 이룬다고 봐 고안한 용어라는 설명이다.

이는 앞서 '삼차각'을 비수학적 개념으로 보거나 '삼차원'을 다르게 표현한 것 뿐이라고 본 다른 연구자들의 시각과는 다르다. 이수정 교수와 오상현 씨는 "이들 해석도 일리가 있지만 삼차각설계도라는 연작시 제목을 실제 시 내용과 설득력있게 연관짓지는 못했다"고 지적했다.

연구팀은 삼차각에 대한 해석을 바탕으로 이상의 '육면각' 단어도 분석했다. 육면각은 삼차각의 적분으로 얻어지는 초입체각으로, 차원상에서 한 점에서 만나는 여섯 개의 면이 이루는 각이라고 봤다. 4차원 도형의 각이라는 얘기다. 4차원 도형은 한 점에서 면 여섯개가 만난다.

연구팀의 '육면각'에 대한 설명. 3차원 입체인 0123에, 4차원상의 다섯번째 점인 4를 더해 5개의 꼭지점을 가진 4차원 도형 01234를 얻었다고 가정하면 이 오면체의 꼭지점 하나는 여섯 개의 면(012, 013, 014, 023, 024, 034)으로 둘러싸인다. 4차원 공간에서 하나의 삼차각 크기는 여섯 개의 면에 의해 정의되는 육면각이다. GIST 제공

연구팀은 '육면각체'는 각진 4차원 도형, '무한육면각체'는 무한히 많은 점으로 이뤄진 4차원 도형을 의미하는 것으로 해석했다. n개(n은 자연수)의 점과 그에 대응하는 육면각으로 이뤄진 도형을 'n-육면각체'라고 부를 수 있기 때문에, 무한육면각체는 4차원상의 임의의 도형을 의미한다고 설명했다.

이런 해석에 따르면 이상의 '건축무한육면각체-AU MAGASIN DE NOUVEAUTES’ 중 ‘사각의중의사각의중의사각의중의사각 의중의 사각’이라는 시구는 공간의 차원을 순차적으로 확장시켜 최종적으로 4차원 공간상에 존재하는 사각형을 구성함을 보여준다.

이 교수와 오씨는 "무한육면각체란 3차원 시공간에서의 임의의 도형, 즉 차원 물체의 시간에 따른 움직임을 4차원 시공간에서 본 것을 말하는 것"이라며 "‘삼차각설계도’와 ‘건축무한육면각체’의 의미는 3차원 물체에 대해 물체의 시간에 따른 변화까지 4차원 시공간에서 설계하고 건축함이라 볼 수 있다"고 논문을 통해 주장했다.

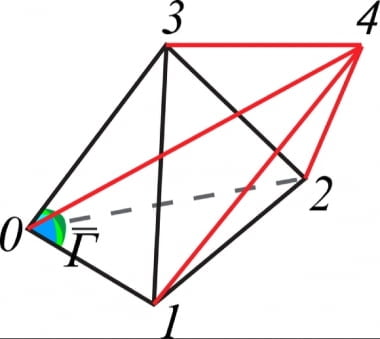
두 연구자는 '삼차각설계도-선에관한각서1' 시에 대해서도 이상이 공간의 차원확장을 시도했다고 봤다. 시 중 '스펙트럼' 점표로 표현된 빛의 스펙트럼을 활용한 해석이다.

이상의 시 삼차각설계도-선에관한각서1

'각서1'의 도식과 '스펙트럼'을 해석한 그림. X·Y·Z축에 빛을 입히는 식으로 이상이 2차원 공간에서 3차원을 표현하려 했다고 해석했다. 사진 GIST

연구팀은 '축X 축Y 축Z' 등 세개의 축을 기반으로 도식의 각 점에 색을 입히면 각 점에서 나오는 빛의 스펙트럼을 활용해 2차원 평면에 3차원 공간을 표현할 수 있다고 설명했다.

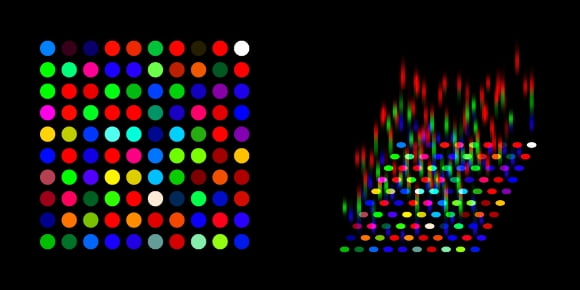
건축과 출신 '천재 시인'…수학·과학 해석 시도 이어져

이상은 서울대 공과대학의 전신 중 일부인 경성고등공업학교 건축과를 졸업한 뒤 건축기사로 일했다. 이때 익힌 건축학적 개념 등을 시에 표현하려다 기존 언어의 한계를 느껴 신조어를 여럿 사용한 것으로 알려졌다.

이상의 시를 해석하기 위해 수학과 과학 등을 접목하는 시도가 이어지는 것도 이래서다. 이수정 교수는 작년 1학기에 개설한 '이상문학과 과학' 수업에서 오상현 씨가 기말 리포트를 통해 제시한 삼차각 관련 아이디어에 주목해 함께 논문 작업을 벌였다.

이수정 교수와 오상현씨는 "이상은 당대 최신 물리학 이론에 대한 이해를 바탕으로 차원상에서 임의의 도형을 설계 건축하는 시도를 연작시에 남겼고, 이 과정에서 삼차각과 육면각체라는 조어를 직접 만들어 사용한 것"이라며 "이번 논문을 통해 이상의 초기시가 상대성이론을 바탕으로 4차원 시공간에서의 설계와 건축을 문학적으로 구현하려는 시도였음을 규명했다"고 밝혔다.

이수정 GIST 교수(왼쪽), 오상현 UC머세드 박사과정생. 사진 GIST

두 연구자는 이어 "이상의 난해시를 파해하기 위한 후속 연구의 디딤돌을 마련했다는 점에서 의의가 있다"라고 덧붙였다. 이 연구결과는 한국어문학국제학술포럼이 발행하는 저널 오브 코리안 컬처 54호에 지난달 31일 게재됐다.

선한결 기자 always@hankyung.com