[재미있는 수학] 수학자들, 수백 년 머리 싸움 끝에 '근의 공식' 발견
입력
수정
지면S12
(5) 삼차·사차방정식의 근
우리가 배우는 수학 내용은 수많은 수학자가 노력하고 투쟁한 끝에 정립한 것입니다. 딱딱한 수학 문제만 풀기보다 수학에 담긴 재미있는 이야기를 접하면서 수학에 대한 흥미와 관심을 먼저 가져보시길 바랍니다.
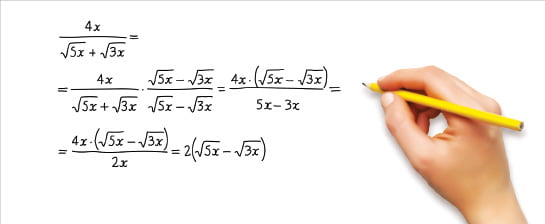
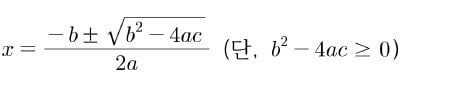
결론적으로 말하면, 삼차·사차방정식에도 근의 공식이 있습니다. 이 공식은 대학에서 수학을 전공할 때 배운 기억이 있는데, 삼차방정식의 근의 공식만 해도 A4 용지 1페이지가 넘어갈 정도로 길고 복잡합니다.
삼차방정식의 해법은 다음 공식을 이용한다.
a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ca)=(a+b+c)(a+bw+cw²)(a+bw²+cw)여기서 w는 방정식 x³=1의 허근 중 하나이므로 w³=1, 1+w+w²= 0 을 만족한다.
…
(후략)
삼차·사차방정식의 근의 공식은 누가, 어떻게 발견했을까요? 이 공식을 발견하기 위한 여러 수학자의 노력은 수학사에서 아주 유명한 이야기입니다.볼로냐 대학의 교수였던 스키피오네 델 페로(1465~1526)는 1500년경 x³+mx=n 꼴의 이차항이 없는 삼차방정식을 풀 수 있는 공식을 발견했습니다. 그러나 그는 학문적 도전을 하는 사람들과의 결전을 위해 공식을 숨기고 있었습니다. 그러다 임종 직전에 제자인 피오르(1506?~?)에만 가르쳐주었죠.
그런데 폰타나(1499~1557)라는 수학자가 x³+px²=n 꼴의 일차항이 없는 삼차방정식에 대한 대수적인 해법을 발견했다고 주장했습니다. 1526년 스승이 사망한 후 피오르는 페로의 업적을 보호하기 위해 폰타나에게 공개적으로 삼차방정식의 해법에 대한 대결을 제안했습니다. 말을 더듬어서 타르탈리아라고 알려진 폰타나는 피오르의 도전을 받아들였고, 서로 삼차방정식 문제 30개씩을 제시해 풀기 대결을 했습니다. 타르탈리아는 여기서 피오르가 제시한 30개의 삼차방정식을 모두 풀며 명성을 얻게 되었습니다.
지롤라모 카르다노(1501~1576)는 책을 집필하던 중 이 대결의 소문을 듣고 삼차방정식의 해법을 배우기 위해 1939년에 타르탈리아에게 만나고 싶다는 편지를 썼습니다. 몇 번에 걸쳐 거절하다 결국 카르다노를 만난 타르탈리아는 이 자리에서 누구에게도 공개하지 않는다는 조건으로 카르다노에게 자신이 발견한 삼차방정식의 근의 공식을 알려주었습니다.몇 년 후 카르다노는 여러 가지 형태의 삼차방정식 해법을 독자적으로 발견해 발표하려고 했지만, 타르탈리아와의 약속 때문에 망설였습니다. 그러다가 페로가 타르탈리아보다 20여 년 전에 삼차방정식의 근의 공식을 발견했다는 사실을 알고 1545년 <위대한 계산법>이라는 책을 통해 삼차방정식과 사차방정식의 근의 공식을 발표합니다.
타르탈리아는 이 소식을 듣고 카르다노를 비난했지만 페로가 삼차방정식의 근의 공식을 먼저 발견한 것이 사실이고, 카르다노가 그의 책에서 발견의 공을 타르탈리아에게 돌렸기 때문에 어찌할 도리가 없었습니다(그러나 공식의 이름은 ‘카르다노의 공식’이라고 합니다).
갑자기 궁금증이 생깁니다. 오차방정식도 근의 공식이 있을까? 16세기 이탈리아 수학자들이 삼차·사차방정식의 해법을 발견한 이래 많은 수학자도 오차방정식의 해를 구하려고 노력했습니다. 그러나 19세기 초까지 그 해법을 발견하지 못했습니다.
노르웨이 수학자 닐스 헨리크 아벨(1802~1829)은 19세기 초에 오차방정식의 해법을 발견했다고 생각했으나 그것은 착오였습니다. 그러나 그는 ‘오차방정식의 해법이 존재할까’라는 의문을 갖게 되었고, 이를 토대로 오차방정식의 일반적인 해법은 계수들의 사칙연산과 제곱 및 제곱근의 연산 범위 내에서는 구할 수 없다는 것을 증명했습니다. 당시 그의 나이는 19세였다고 합니다. 아벨은 희망하던 교수가 되지 못하고 가난과 결핵에 시달리다 27세를 넘기지 못하고 요절했습니다.